When things get complicated, the researcher feels really challenged: She tries to find out to what extent the conservation laws of physics can be set up in the form of mathematical equations – and to what extent these are suitable for describing turbulent flows in fluids.
When Dr Martina Hofmanová thinks about flows in fluids, she is not sitting in a laboratory shooting water through tubes. Instead, she is at her desk, bent over a sheet of paper with equations written on it – often all day, if time permits. “This is really my passion and gives me an extraordinary amount of pleasure,” says the professor of mathematics at Bielefeld University.
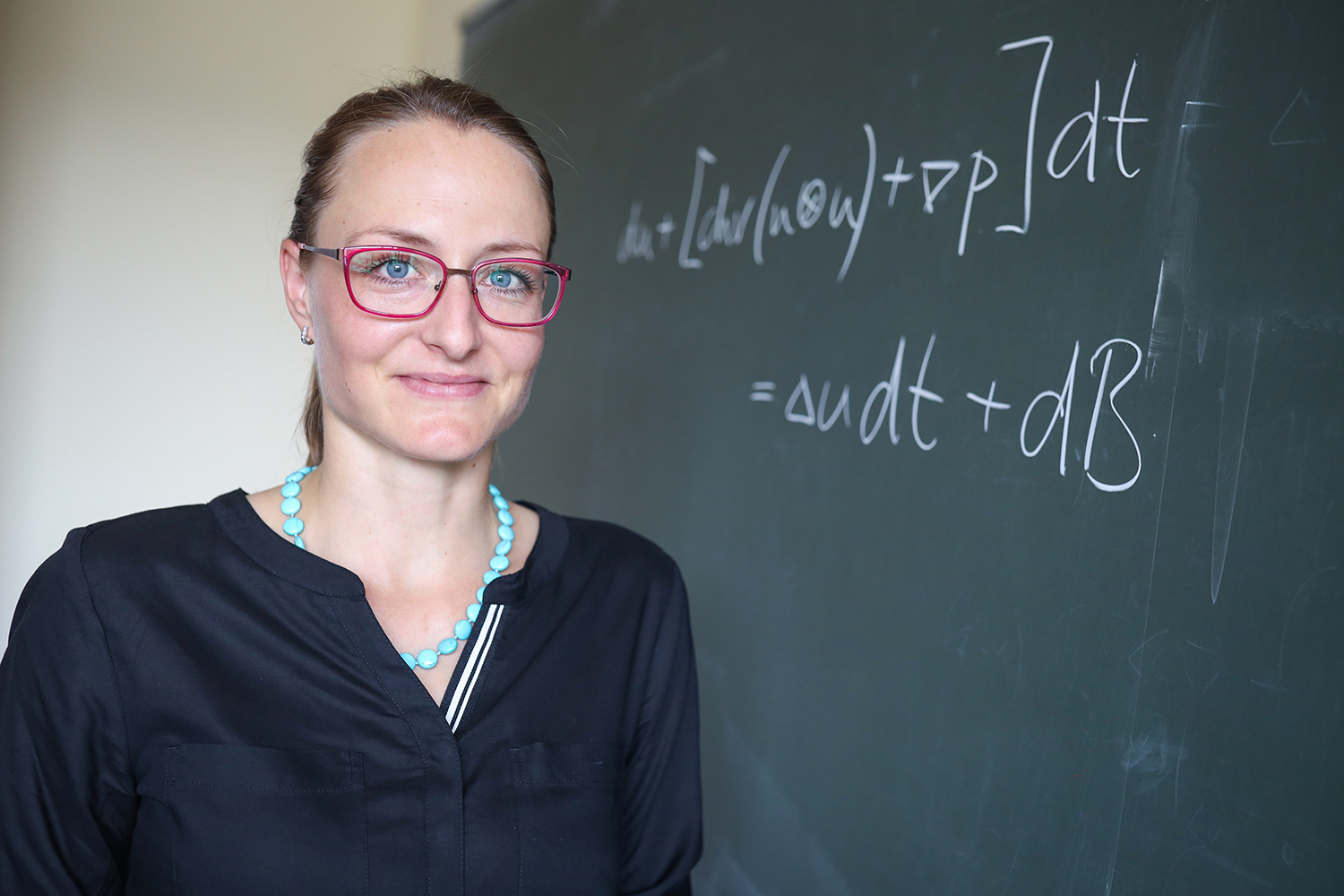
© Bielefeld University / S. Jonek
The researcher focuses on fluid mechanics and stochastic partial differential equations. In short, she studies how randomness affects the flow of fluids – and to what extent this can be calculated. “I work with equations from physics and want to find out to what extent there are mathematical solutions,” she says.
For her project “Mathematical analysis of fluid flows: The challenge of randomness”, she received an ERC Starting Grant of 1.5 million euros in 2021, which is awarded to top young researchers. The project will run until 2026. “My goal is to find the appropriate equations to describe such flows and to find out whether these equations have a solution,” says the mathematician. “And the question is not only whether there is a solution, but above all whether a solution is unique.”
Sometimes physical equations lead to solutions that cannot be correct at all – but which are correct within the equation. “If there is a glass of water on the table and I stir it, I expect the water to start moving and there will be turbulence,” says the professor. But what if the water starts to move on its own, without any external influence? “That is not possible,” says Hofmanová. “But the physical equations provide such a solution.”
Her aim is to find out how the equations can be modelled in such a way that the solutions are accurate or how possible solutions can be better estimated. “Such equations are also used, for example, to calculate meteorological models,” she says. Weather models consider a large number of factors that often influence each other. “For the calculations, it is important to be able to distinguish which solutions are actually possible and which are not.
Because not only probabilities play a role, but also randomness, randomness also finds its way into the equations – at least sometimes. “In the Collaborative Research Centre 1283, in which I am involved, we are investigating the role of random influences and whether we get better results if we include certain types of randomness in the equation.” Randomness that is self-perpetuating, such as when turbulence develops and one particle in a fluid sets the next one in motion, creating chaotic eddies, is also known as stochastic noise. “Actually, in some situations and for some questions we could indeed profit from a suitable noise, but there is not an improvement in every case.”
The solutions to these equations are not only important for meteorology, but also for many other fields: If it is possible to calculate, avoid or even exploit turbulence, this can have a positive effect on the flight behaviour of aircraft or for space travel. “At the moment, however, it’s all about basic research,” says Hofmanová. Engineers and applied physicists use the equations for real simulations, whether or not there is a solid mathematical theory for them. For the scientist, there is currently no point in testing the equations in the laboratory under real conditions – at least not yet. “The next step would be to simulate the flows on the computer.”
It is not always possible to get to the bottom of an equation on paper. To develop new ideas and let her mind wander, the researcher likes to ride her road bike around Bielefeld. “I can really switch off on the bike and I like to ride for hours,” she says. There is not much time for that these days, however, as the researcher likes to spend a lot of time with her almost two-year-old daughter, whom she is raising with her husband. By the end of her schooling, Hofmanová knew she wanted to study mathematics. “Mathematics has always been much easier for me than for others,” she says, “so I thought I should take advantage of that.” Later in her studies, she had a slightly harder time deciding whether to specialise in financial mathematics or probability theory. “I felt that probability theory was more difficult – and that challenged me.” She feels very much at home in Bielefeld, where she has been conducting research in the field since 2017. “The Faculty of Mathematics is very research-oriented, which is very conducive to my work and something I really appreciate.”





